Строй-Техника.ру
Строительные машины и оборудование, справочник
Для решения многих задач динамики может быть использован принцип Д’Аламбера, согласно которому в любой момент времени имеет место равновесие сил инерции, активных внешних сил и сил реакций связей находящейся в движении системы.
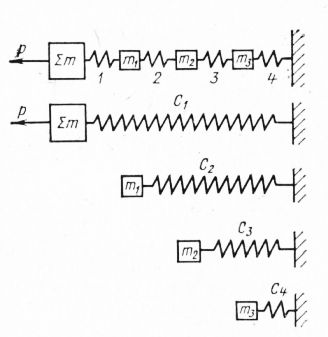
Рис. 1. Эквивалентная схема ковшовой цепи с ковшами для случая стопорения при решении задач методом суперпозиции
Рекламные предложения на основе ваших интересов:
Дополнительные материалы по теме:
Рис. 2. Схема к расчету колебаний бадьи или ковша на канате при разгрузке
Если система материальных точек находится в равновесии, то работа всех сил на любых малых перемещениях, при которых не нарушаются наложенные на систему связи, равна нулю. Такое перемещение материальных точек системы в механике называют возможным.
Таким образом, сумма работ всех сил как внутренних, так и внешних, приложенных к системе, и сил инерции на произвольном совместимом со связями перемещении равна нулю.
В качестве примера приведем конец поворота вращающейся платформы крана или драглайна, когда внезапное торможение приводит к снижению скорости вращения, а тяговый канат драглайна свободно провисает. Расчетная схема, соответствующая этому условию, представлена на рис. 3.
Составление уравнения движения связано в этом случае с достаточно громоздкими вычислениями. Это обстоятельство ограничивает практическое применение принципа Д’Аламбера — Лагранжа.
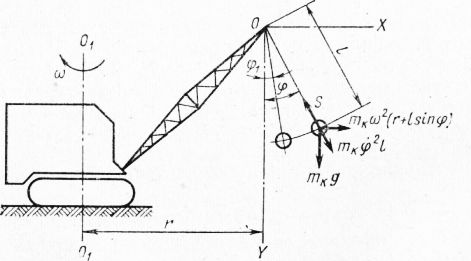
Рис. 3. Расчетная схема крана или драглайна при торможении в процессе поворота вращающейся платформы
Наиболее удобным и простым методом решения задач динамики для несвободных систем является метод Лагранжа, основанный на понятии обобщенных координат. Движение системы исследуется в обобщенной системе координат, т. е. в независимых один от другого параметрах, изменение которых в функции времени полностью определяет движение системы. Число этих параметров равно числу степеней свободы системы и соответствует числу уравнений Лагранжа. Для получения дифференциальных уравнений движения методом Лагранжа необходимо составить выражение для кинетической и потенциальной энергии системы в функции выбранных обобщенных координат.
Если на систему действуют силы или моменты упругости, а также вес (так называемые консервативные силы), то работа, производимая ими, определяется только начальным и конечным положением системы независимо от траектории движения. Поэтому обобщенная сила в этом случае может быть определена как частная производная от потенциальной энергии системы по соответствующей обобщенной координате, взятой с обратным знаком, т. е. где их неконсервативная составляющая обобщенной силы.
Применим метод Лагранжа к случаю внезапной разгрузки ковша драглайна, соответствующему ранее рассмотренной схеме.
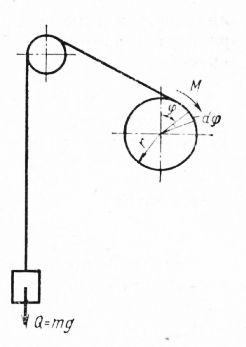
Рис. 4. Схема действия сил при подъеме груза лебедкой
Таким образом, получено уравнение, к которому мы ранее пришли бы при решении задачи методом вероятных перемещений.
Методика составления уравнений движения систем с распределенной массой в принципе аналогична рассмотренным выше методам, но и не лишена определенной специфики.
Составление уравнения колебаний для цепного рабочего органа многоковшовых экскаваторов, драг, элеваторов, тяговых . цепей транспортеров и т. д. существенно упрощается, если допустить, что цепной рабочий орган в отношении протекающих в нем динамических процессов эквивалентен однородному по длине упругому стержню. Хотя цепной рабочий орган, как известно, имеет конечное число степеней свободы, равное числу сосредоточенных масс, а у упругого стержня число степеней свободы бесконечно, тем не менее при решении задач динамики цепного рабочего органа его можно рассматривать как однородный по длине упругий стержень.
К системам с распределенной массой может быть отнесен канат, когда при большой длине масса его соизмерима с массой приводимой им в движение конструкции или поднимаемого груза.
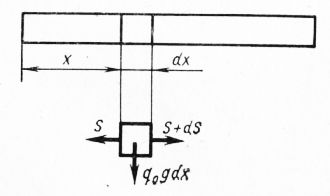
Рис. 4. Схема эквивалентного упругого стержня
Учет внутренего трения в процессе переходного периода рассмотрим на примере канатной системы управления. В системе полиспаст — лебедка при импульсивной нагрузке в канате вследствие деформации последнего дополнительно затрачивается работа на трение ATV каната о канат при многослойной навивке и каната о барабан при однослойной навивке. Рассмотрим элементарный участок длины каната, набежавшего на барабан. При возрастании импульсивной нагрузки от нуля до Ря работа трения может быть определена следующим образом.
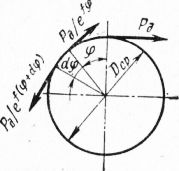
Рис. 5. Схема к определению работы трения каната о барабан при импульсивной нагрузке
Как указывалось, Фохт приписывает силам трения вязкий характер, что позволяет предельно упростить дифференциальное уравнение движения, считая вязкие сопротивления пропорциональными скорости движения.
Полученные уравнения движения системы соответствуют затухающим колебаниям, причем с достаточно медленным изменением амплитуды свободных колебаний, поскольку демпфирование, вызванное силами внутреннего трения, как правило, не очень велико. Для составления уравнения движения системы в переходном процессе необходимо знать закон изменения внешнего момента, приложенного к рассматриваемой системе.
Рассмотрим случай пуска ленточного транспортера с приводом от асинхронного двигателя переменного тока с фазовым ротором и контактными кольцами. При пуске транспортера производится ступенчатое выведение секций добавочных сопротивлений в цепи двигателя. В первом приближенйи примем, что реостатные характеристики асинхронного двигателя прямолинейны. На приведенной характеристике электродвигателя M—f(со) приняты следующие обозначения: М’ — наибольший момент, развиваемый двигателем на каждой ступени реостата; М — момент, развиваемый двигателем при переключении реостата на следующую ступень; со0 — синхронная угловая скорость вращения вала электродвигателя.
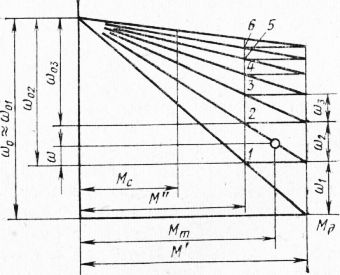
Рис. 6. Характеристика асинхронного электродвигателя в пусковом режиме
Рекламные предложения:
Главная → Справочник → Статьи → Форум
Механизация земляных работ
Механизация строительства
Механизация дорожных работ
Автоматизация строительства
→ Бетонные работы
→ Мини-тракторы
 Разделы
Разделы
Строительные машины и оборудование
→ Для специальных земляных работ
→ Дорожно-строительные машины
→ Строительное оборудование
→ Асфальтоукладчики и катки
→ Большегрузные машины
→ Строительные машины, часть 2,
→ Дорожные машины, часть 2
→ Ремонтные машины
→ Ковшовые машины
→ Автогрейдеры
→ Экскаваторы
→ Бульдозеры
→ Скреперы
→ Грейдеры
Эксплуатация строительных машин
→ Эксплуатация средств механизации
→ Эксплуатация погрузочных машин
→ Эксплуатация паровых машин
→ Эксплуатация экскаваторов
→ Эксплуатация подъемников
→ Эксплуатация кранов перегружателей
→ Эксплуатация кузовов машин
→ Крановщикам и стропальщикам
Ремонт строительных машин
Ремонт дорожных машин
Ремонт лесозаготовительных машин
Ремонт автомобилей КАмаЗ
Техническое обслуживание автомобилей
Очистка автомобилей при ремонте
Материалы и шины
Остались вопросы по теме:
"Методы составления и решения уравнении движения системы"
— воспользуйтесь поиском.
→ Машины городского хозяйства
→ Естественная история машин
→ Транспортная психология
→ Пожарные автомобили
→ Автомобили-рефрижераторы
→ Монтаж и эксплуатация лифтов
→ Тракторы