Строй-Техника.ру
Строительные машины и оборудование, справочник
В ранние годы автомобилестроения, когда были широко распространены коробки передач со скользящими шестернями, а конструкции фрикционных сцеплений еще не достигли достаточной степени совершенства, нередко наблюдался выход из строя вследствие разрушения торцов зубьев от ударов при их включении. Этот вид повреждения теперь практически устранен благодаря улучшению качества как сцеплений, так и шестерен. В конструкциях коробок передач с постоянно сцепленными шестернями подобный дефект вообще невозможен ввиду отсутствия скользящих шестерен.
Шестерни современных автомобильных коробок передач могут выходить из строя или по причине поломки зубьев в результате воздействия чрезмерных изгибающих усилий, или вследствие разрушения рабочих поверхностей зубьев — образования раковин (питтинг) и бороздчатого износа, (скоринг),. вызываемых чрезмерными -напряжениями сжатия на этих поверхностях. Поломки зубьев были обычным видом повреждений в период, когда применялись зубья нормальной высоты, а шестерни изготовлялись из материалов сравнительно невысокой прочности. Каждый зуб шестерни, находящийся в контакте с зубом сопряженной шестерни, работает как консольная балка, нагруженная силой, приложенной в точке контакта. Изгибающий момент, вызываемый этой нагрузкой, имеет наибольшее значение у основания зуба и изменяется в зависимости от расстояния между точкой контакта и основанием зуба. Напряжение изгиба у основания зуба обратно пропорционально квадрату толщины зуба в этом сечении. Способность шестерен противостоять изгибающим усилиям значительно возросла благодаря применению укороченных зубьев с увеличенным углом зацепления, улучшению материалов, применяемых для изготовления шестерен, и их термической обработки. Тем не менее при конструировании зубчатых передач рекомендуется проверять размеры шестерен путем расчета зубьев на изгиб по максимальному крутящему моменту, для которого передача предназначается.
При расчетах зубьев шестерен на прочность всегда предполагается, что нагрузка равномерно распределена по всей длине зуба (т. е. по ширине шестерни); однако практически вследствие неточности обработки шестерен или деформации валов и картера под нагрузкой этого не бывает. Наблюдения показывают, что при поломке зубьев плоскость разрушения обычно непараллельна оси шестерни, и это подтверждает предположение о неравномерности распределения нагрузки по длине зуба.
Рекламные предложения на основе ваших интересов:
Дополнительные материалы по теме:
С тех пор как коробки передач выполняются более компактными и напряжения сжатия на поверхности контакта зубьев повысились, повреждение шестерен вследствие образования раковин
стало более частым явлением, поэтому расчет зубьев шестерен на поверхностное сжатие приобретает большее значение, чем расчет зубьев на изгиб. Раковины и бороздчатый износ на поверхности зубьев образуются главным образом вблизи начальной окружности1. Эти разрушения поверхности нарушают профиль зубьев и вызывают шум при работе шестерен. Возникновение этих явлений сокращает срок службы шестерен.
Формула Льюиса. Прочность зубьев шестерен на изгиб определяется по формуле, которая была впервые предложена Льюисом в докладе, прочитанном в Инженерном обществе Филадельфии в 1893 г.
Льюис исходил из предположения, что вся нагрузка воспринимается одной парой зубьев, причем нагрузка приложена к вершине зуба. В отношении современных зубчатых колес это предположение приводит к большой ошибке в сторону повышения запаса прочности, так как в тот момент, когда один зуб ведущей шестерни выходит из зацепления с зубом сопряженной шестерни (т. е. в момент касания с ним у вершины), следующий зуб ведущей шестерни уже в течение некоторого промежутка времени находится в зацеплении и воспринимает большую часть нагрузки. Но„ с другой стороны, формула Льюиса не учитывает концентрации напряжений, которая всегда имеет место в точках резкого изменения сечения (в данном случае у основания зуба), и это в большей или меньшей степени компенсирует неточность первого допущения формулы. В настоящее время стало возможным определить как наиболее высокое положение точки соприкосновения в период, когда вся нагрузка передается одной парой зубьев, так и степень увеличения напряжений, вызванного резким изменением сечения у основания зуба_Учет этих двух факторов позволяет определить более точно возникающие в зубьях максимальные напряжения.
Следует отметить, что расчету на прочность должна подвергаться меньшая из пары совместно работающих шестерен, потому что она всегда является более слабой и в отношении сопротивления изгибу и в отношении сопротивления смятию поверхности зуба.
Очевидно, что зуб ведущей шестерни подвергается наибольшим изгибающим напряжениям как раз в тот момент, когда в зацепление начинает вступать последующая пара зубьев. Это положение показано на рис. 1, где изображена ведущая шестерня с 15 зубьями в зацеплении с ведомой шестерней, имеющей 30 зубьев. Зубья шестерен — укороченного типа, с углом зацепления 20°.
Вновь вступающий в зацепление зуб ведущей шестерни начинает касаться зуба ведомой шестерни в точке А, лежащей на основной окружности ведущей шестерни. Точка касания перемещается затем в направлении к вершине зуба ведущей шестерни. Непосредственно перед этим моментом средний из трех показанных на чертеже зубьев передавал всю нагрузку один, и точка В является наиболее высокой точкой его профиля, в которой прилагается полная нагрузка. Хотя точка соприкасания и продолжает перемешаться к вершине зуба, однако в этот период некоторая часть нагрузки воспринимается уже новым зубом, вошедшим в зацепление. Таким образом, зуб ведущей шестерни подвергается действию максимального изгибающего момента, когда касание зубьев происходит в точке В.
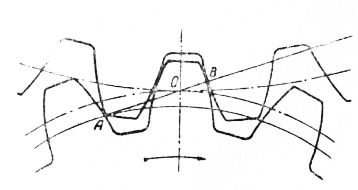
Рис. 1. Схема, показывающая высшую точку приложения силы, когда в зацеплении находится одна пара зубьез.
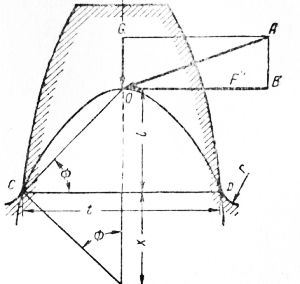
Рис. 2. Схема для расчета зуба шестерни на изгиб.
Расчет зубьев на изгиб. На Рис. 2 в увеличенном масштабе показан зуб, передающий полную нагрузку. Отрезок прямой OA по величине и направлению представляет собой силу, действующую на зуб. Эта сила может рассматриваться как приложенная в любой точке внутри контура зуба вдоль линии зацепления. Будем считать ее приложенной в точке О, являющейся точкой пересечения линии зацепления с осью зуба, так как это упрощает определение напряжения изгиба. Тогда ОВ будет составляющей давления на зуб, параллельной опасному (слабейшему) сечению зуба. Обозначим эту составляющую через F’. Величина ее может быть определена по крутящему моменту, передаваемому шестерней, и расстоянию от оси шестерни до точки О.
Впишем теперь в контур зуба параболу, имеющую вершину в точке О и касающуюся профиля зуба близ его основания. Эта парабола представляет сечение консольной балки равного сопротивления изгибу. Линия CD, соединяющая точки касания параболы к контуру зуба, показывает слабейшее сечение зуба. Разрушение зуба под действием изгибающих усилий будет происходить, как правило, по этому сечению. Отклонения от этого могут быть вызваны несовершенством механической обработки или неоднородностью материала шестерни.
Это напряжение в слабейшем сечении определено по изгибающему моменту, создаваемому касательной силой F. Однако действительная сила, приложенная к зубу (нормальная к профилю зуба в точке касания), представляется через OA, а ОВ является касательной составляющей этой силы. На зуб действует также радиальная составляющая OG, которая создает напряжения сжатия в слабейшем сечении или, вернее, создавала бы напряжения сжатия, если бы действовала одна. Поломка зуба происходит всегда в результате чрезмерных напряжений растяжения, действующих в точке D слабейшего сечения. Напряжение растяжения в этой точке от действия изгибающего момента, создаваемого касательной составляющей ОВ, очевидно, уменьшается под действием сжатия от радиальной составляющей OG; однако при расчетах зуба на прочность этот эффект обычно не учитывается.
Коэффициент формы и числа зубьев. Коэффициент z, который может быть назван коэффициентом формы и числа зубьев, не зависит от питча, но изменяется в зависимости от числа зубьев ведущей шестерни, а также от числа зубьев сопряженной с ней ведомой шестерни.
В предыдущих уравнениях через F’ обозначалась тангенциальная сила, приложенная в точке О пересечения линии зацепления с осью зуба. Эту силу довольно трудно определить в каждом частном случае, так как для этого необходимо сначала определить положение точки О путем построения чертежа, подобного рис. 1, для рассматриваемой пары шестерен. На рис. 63 точка О очень близка к начальной окружности. Однако, когда сопряженные шестерни имеют малые числа зубьев, эта точка будет расположена вне начальной окружности на заметном от нее расстоянии. Более удобно пользоваться окружной силой F, действующей по начальной окружности, .потому что радиус начальной окружности всегда известен. Если точка О расположена вне начальной окружности, то окружная сила по начальной окружности больше, чем F, и это может быть компенсировано пропорциональным уменьшением коэффициента г.
Значения коэффициента z с поправкой на разницу между расстоянием от центра шестерни до точки О и радиусом начальной окружности для шестерен значительного диапазона числа зубьев (ведущей и ведомой шестерен), имеющих зуб, укороченным в соответствии с американским стандартом, приведены на графике рис. 3.
Концентрация напряжений у основания зуба. Повышение напряжений вследствие резкого увеличения сечения у основания зуба, по-видимому, не поддается аналитическому определению.
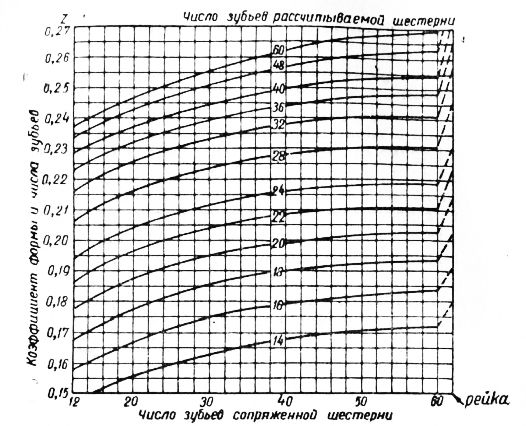
Рис. 3. Коэффициент формы и числа зубьев для стандартного укороченного зуба.
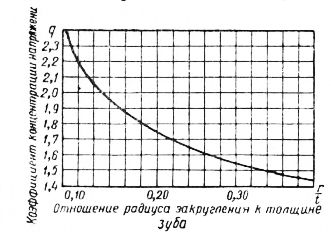
Рис. 4. Кривая коэффициента концентрации напряжений.
q — коэффициент концентрации напряжений определяемый
Прочность косозубых шестерен. Анализ напряжений в зубьях кооозубых шестерен исключительно сложен, так как линия соприкасания перемещается не параллельно образующей боковой поверхности зуба, а под некоторым углом к ней, пересекая ееКогда на ведущей шестерне косозубой передачи движущаяся впереди часть зуба выходит из зацепления, в зацепление начинают входить последовательно следующие за ней его части, а так как у ведущей шестерни касание начинается на нижней части зуба и кончается у вершины его, то линия касания всегда образует некоторый угол с образующей зуба. Кроме того, на способность косого зуба противостоять изгибающим усилиям, несомненно, оказывает положительное влияние то, что его основание представляет собой не плоскую поверхность, а следует своими очертаниями цилиндрической поверхности тела (обода) шестерни.
Далее в косозубых шестернях нагрузка на отдельные зубья повышается и снижается более плавно. По указанным причинам представляется возможным считать, что косозубые шестерни, будут надежно передавать окружные силы той же величины, что и прямозубые шестерни с тем же диаметром начальной окружности и той же шириной шестерни, имеющие зубья того же нормального Диаметрального питча. Тогда расчет на прочность косозубых шестерен может производиться при помощи тех же формул, которые были выведены ранее для прямозубых цилиндрических шестерен.
Напряжение сжатия на поверхности зубьев.
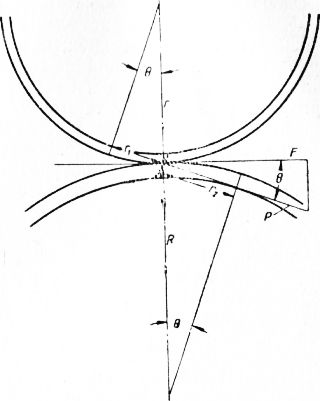
Рис. 5. Схема для определения радиусов кривизны эвольвентных профилей зубьев в точке касания.
Сопротивление смятию материалов зубчатых колёс. Данных относительно сопротивления смятию различных материалов имеется немного. Проф. Штрибек, который является одним из пионеров в разработке теории шарикоподшипников, нашел, что хромистая сталь, применяемая для изготовления шариков подшипников, подвергнутая специальной термической обработке, имеет предельное сопротивление смятию, равное 45600 кг/см2; при другой термообработке сопротивление смятию составляло 48 250 кг/см2.
Если приведенное выше уравнение дает действительное значение предельного сопротивления смятию материала зубьев, то шестерни, спроектированные в соответствии с существующей практикой, будут иметь значительный запас прочности.
Однако эти напряжения соответствуют статической нагрузке. Напряжения от динамической нагрузки, возникающей при работе шестерен на больших скоростях, будут значительно выше. В практике расчета зубчатых передач принято учитывать влияние динамического приложения нагрузки введением коэффициента увеличения нагрузки.
Величины максимального допускаемого удельного давления для различный сталей, применяемых для изготовления шестерен разных назначений, были предоставлены автору Уикенденом (Интернейшенел Никель Компани, Канада): для цементованной стали с 3,5% никеля при работе с перерывами (как, например, на автомобиле) — 14 100 кг/см2-, для закаленных в масле шестерен из сталей SAE 2350 и 3250 при периодической работе—11 280 кг/см2; для цементованных сталей SAE 4615 и 2315, также при периодической работе— 14 100 кг/см2 и для цементованных сталей SAE 2512 и 4815— 15 500 кг/см2. При непрерывной работе шестерен под нагрузкой предельное допускаемое сопротивление смятию должно быть снижено приблизительно на 25%. В связи с этим следует подчеркнуть, что максимальное сопротивление смятию, которое могут выдержать зубья шестерен, зависит не только от материала шестерен, но и от примененной смазки. Из различных типов зубчатых колес, применяемых в автомобиле, наибольшее количество повреждений поверхности от образования раковин и бороздчатого износа наблюдается у гипоидных шестерен заднего моста, где напряжения смятия очень высоки и где имеет место большее скольжение (а следовательно, больше выделяется тепла при одинаковых условиях нагрузки и скорости вращения), чем у обычных цилиндрических прямозубых и косозубых шестерен. Для гипоидных шестерен теперь, как правило, применяются так называемые смазки Е. P. (Extreme Pressure), которые предотвращают возникновение большинства поверхностных разрушений.
Приведенные выше значения максимального допускаемого (безопасного) удельного давления для шестерен из различных сталей относятся к простым смазкам нефтяного происхождения.
Число зубьев, находящихся в зацеплении. Чтобы работа шестерен была плавной и непрерывной, каждая последующая пара зубьев должна вступить в зацепление раньше, чем предыдущая пара зубьев выйдет из зацепления. Действительно, чем больше перекрытие периодов соприкасания зубьев, тем более плавной будет работа шестерен.
На рис. 6 линия зацепления касается обеих основных окружностей. Зацепление начинается в точке В пересечения линии зацепления с окружностью выступов ведомой шестерни и кончается в точке Е пересечения линии зацепления с окружностью выступов ведущей шестерни.
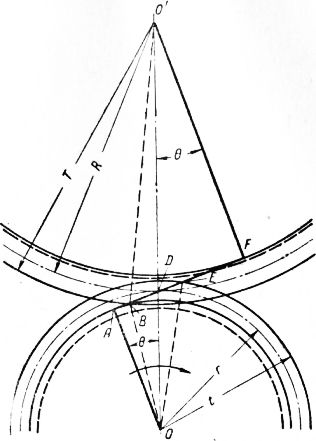
Рис. 6. Схема для определения рабочей длины линии зацепления.
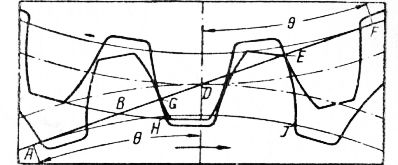
Рис. 7. Схема для определения величины основного шага.
На рис. 7 показаны две одинаковые шестерни с 24 укороченными зубьями, находящиеся в зацеплении. Из приведенного выше выражения для этого случая находим, что ns =1,315, что соответствует по схеме отношению BE к GE.
Значительного улучшения плавности работы можно ожидать, если число пар зубьев, находящихся в зацеплении, будет больше двух .Тогда нагрузка все время будет распределяться не менее чем между двумя парами зубьев (в действительности не поровну), тогда как при числе пар зубьев в зацеплении, меньшим двух, нагрузка! в некоторые моменты будет восприниматься только одной парой зубьев. Следует заметить, однако, что опыты, проведенные одной крупной фирмой с шестернями коробок передач, имеющими по расчету в зацеплении одновременно две пары зубьев и нарезанными обычными методами, показали не вполне удовлетворительные результаты. Очевидно, ошибки в определении шага были таковы, что не позволили получить ожидаемого распределения нагрузки между двумя парами зубьев.
Изменение профиля зуба. На практике число пар зубьев, одновременно находящихся в зацеплении, часто уменьшается вследствие изменения профиля зуба. Точно изготовленные эвольвентные шестерни (если они установлены на правильном расстоянии и если шестерни и опоры абсолютно жестки) должны работать совершенно плавно.
Однако в действительности эти условия не выполняются, в результате чего наблюдается стремление врезания кромки вершины зуба в зуб сопряженной шестерни. Это явление вызывает шум и неплавную работу передачи.
Для предотвращения этого профиль зуба видоизменяют таким образом, что часть, расположенная вблизи вершины и составляющая более ‘Д высоты головки, является также эвольвентной, но с большим углом зацепления, чем рабочая часть профиля зуба.
Прежде подобное видоизменение профиля сводилось к фланкированию вершины и первоначально было введено главным образом для устранения врезания зуба в зуб сопряженной шестерни вследствие неточности профиля зуба или шага С повышением точности изготовления зубчатых колес такое фланкирование вершины стало менее необходимым. В настоящее время необходимость в изменении профиля зуба возникает в основном вследствие деформации зубьев под нагрузкой, увеличившейся вместе с удельной нагрузкой на зуб в связи со стремлением уменьшить размеры коробки передач в отношении передаваемого крутящего момента. Недавно проведенные в Англии исследования привели к заключению, что измененный контур, лежащий внутри эвольвентного профиля у вершины зуба, должен переходить в эвольвенту в точке, соответствующей точке на линии зацепления, отстоящей на один основной шаг от пересечения линии зацепления с окружностью выступов сопряженной шестерни. Сужение измененной части профиля У вершины зуба должно быть одинаковым у обеих зацепляющихся шестерен и равным сумме статических деформаций зубьев ведущей и ведомой шестерен под полной нагрузкой в определенный момент зацепления. Этот момент должен соответствовать зацеплению зубьев в точке, отстоящей по линии зацепления на один основной шаг от пересечения линии зацепления с окружностью выступов одной из шестерен (границы зоны работы одной пары зубьев).
Эллиптоидные (бочкообразные) зубья. При расчетах на прочность всегда принимают, что нагрузка равномерно распределяется по всей длине зуба. Однако в действительности этого никогда не бывает. Если изношенные шестерни подвергнуть точной проверке, то окажется, что соприкасание зубьев происходит только на одном конце или, по крайней мере, оно на одном конце интенсивнее. Такое неправильное касание может быть вызвано нарушением соосности валов агрегата, прогибом валов под нагрузкой, большими неточностями изготовления шестерен или короблением шестерен при термообработке. Смещение контакта к краю зуба, несомненно, вызывает концентрацию напряжений и уменьшает срок службы шестерен. В целях предотвращения смещения контакта к краю зуба фирмы Нейшенел Броуч энд Мэшин Компани в Детройте разработала метод чистовой обработки; шестерен, при котором боковым поверхностям зубьев придается очень небольшая кривизна в продольном направлении. Боковые поверхности зубьев в сечениях^ получают эллиптическую форму, толщина зубьев у краев меньше,* чем в середине, приблизительно на 0,013 мм. Такая форма получается при чистовой обработке шестерни путем придания рабочему столу шевинговального станка качательного движения.
Эллиптоидная (бочкообразная) форма может быть придана зубьям цилиндрических шестерен как прямозубых, так и косозу-бых, причем у последних она может быть получена также посредством шлифования. Для шлифования эллиптоидных шестерен употребляется метод фасонного круга и шлифовальный круг, управляемый соответствующим кулачковым механизмом, производит шлифование у краев зуба на несколько большую глубину, чем у середины. Как правило, только одна из пары сопряженных шестерен выполняется с эллиптоидными зубьями.
Скорость скольжения между зубьями шестерен в любой точке линии зацепления может быть быстро определена графическим путем. Согласно рис. 70 точка А, в которой начинается зацепление вубьев, является точкой пересечения окружности выступов ведомой шестерни с касательной АС к обеим основным окружностям1’ По скорости вращения ведущей шестерни и диаметру ее основной окружности можно найти окружную скорость этой точки, которая изобразится отрезком ВА, касательным к основной окружности в точке А. Далее измеряем расстояние от точки зацепления зуба ведомой шестерни до центра этой шестерни, т. е. радиус окружности, описываемый рассматриваемой точкой. Зная этот радиус и число об/мин ведомой шестерни, подсчитываем окружную скорость указанной точки и откладываем ее на чертеже в виде отрезка прямой DA, касательной к окружности выступов ведомой шестерни в точке зацепления. Обе окружные скорости откладываются, конечно, в одинаковом масштабе. Тогда отрезок DB, соединяющий концы векторов окружных скоростей, будет представлять собой по величине и направлению скорость скольжения зубьев.
Деля линию зацепления на равные части, мы можем определить скорость скольжения между зубьями в каждой точке деления и изобразить это графически, нанеся расстояния по линии зацепления на оси ординат. Когда зубья соприкасаются в полюсе зацепления, скольжение отсутствует, так как касательные к окружностям, описываемым точками соприкасания зубьев обеих шестерен, совпадают. В результате получается график, представленный на рис. 9. Скорость скольжения (трения) изменяется в прямой зависимости от расстояния по линии зацепления. Она равна нулю в полюсе зацепления и в этой точке меняет направление.

Рис. 8. Графическое определение скорости скольжения зубьеа шестерен.
Приведенные на рис. 9 данные относятся к паре шестерен с 15 и 30 зубьями, с питчем и углом зацепления 14°30’ при скорости вращения ведущей шестерни 1000 об/мин. Осевая линия на левой стороне графика соответствует основной окружности ведущей шестерни, и легко видеть, что здесь скорость скольжения меньше, чем у вершины зуба ведущей шестерни (осевая линия на оравой стороне графика).
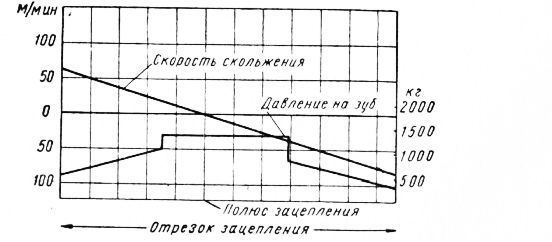
Рис. 9. Диаграмма изменения скорости скольжения и давления на зуб .по линии зацепления.
Рекламные предложения:
Главная → Справочник → Статьи → Форум
Механизация земляных работ
Механизация строительства
Механизация дорожных работ
Автоматизация строительства
→ Бетонные работы
→ Мини-тракторы
 Разделы
Разделы
Строительные машины и оборудование
→ Для специальных земляных работ
→ Дорожно-строительные машины
→ Строительное оборудование
→ Асфальтоукладчики и катки
→ Большегрузные машины
→ Строительные машины, часть 2,
→ Дорожные машины, часть 2
→ Ремонтные машины
→ Ковшовые машины
→ Автогрейдеры
→ Экскаваторы
→ Бульдозеры
→ Скреперы
→ Грейдеры
Эксплуатация строительных машин
→ Эксплуатация средств механизации
→ Эксплуатация погрузочных машин
→ Эксплуатация паровых машин
→ Эксплуатация экскаваторов
→ Эксплуатация подъемников
→ Эксплуатация кранов перегружателей
→ Эксплуатация кузовов машин
→ Крановщикам и стропальщикам
Ремонт строительных машин
Ремонт дорожных машин
Ремонт лесозаготовительных машин
Ремонт автомобилей КАмаЗ
Техническое обслуживание автомобилей
Очистка автомобилей при ремонте
Материалы и шины
Остались вопросы по теме:
"Расчет шестерен"
— воспользуйтесь поиском.
→ Машины городского хозяйства
→ Естественная история машин
→ Транспортная психология
→ Пожарные автомобили
→ Автомобили-рефрижераторы
→ Монтаж и эксплуатация лифтов
→ Тракторы