Случай 1 — один конец каната закреплен, другой натягивается натяжным грузом.

Случай 2 — один конец каната закреплен, другой конец натягивается качающейся опорной башней.

В рассматриваемом случае качающаяся башня, поворачиваясь вокруг опорного шарнира, своим весом натягивает пучок канатов (несущего и рабочих), причем натяжение канатов изменяется в зависимости от веса грузовой тележки и положения ее в пролете. Однако изменения эти невелики и в обычных кранах не превышают 10%.

На рис. 47, а, б я в стрелками отмечены различные положения грузовой тележки в пролете и соответствующие положения качающейся башни. Наибольшее натяжение канатов возникает при наиболее близком положении груженой тележки от качающейся башни, когда давление, передаваемое на качающуюся башню, также достигнет наибольшего значения. Тогда башня отклонится своей вершиной из пролета на максимальную величину и плечи всех вертикальных сил (реакций от тележки и канатов и собственного веса башни с противовесом) увеличатся.

Рассмотрим условия равновесия башни для различных положений тележки в пролете крана (рис. 48).

Обычно при расчете за исходное положение качающейся башни .принимают такое, при котором задняя стойка ее вертикальна и тележка находится у головки некачающейся башни (см. рис. 47, а).

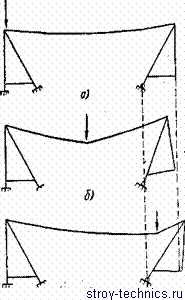
Рис. 47. Положения качающейся опорной башни кабельного крана в зависимости от положения грузовой тележки в пролете.

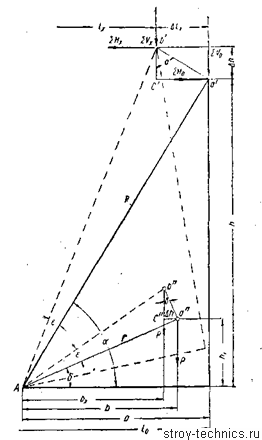
Рис. 48. Схема сил, прикладываемых к качающейся башне кабельного крана.

Пользование таким упрощенным уравнением обусловливает погрешность в значении 2% до 3%.

Угол а, вводимый в рассмотренные уравнения, образуется горизонталью и прямой, соединяющей шарнир А с точкой пересечения равнодействующих вертикальных и горизонтальных составляющих натяжения канатов. Так как обычно стремятся, чтобы указанные равнодействующие пересекались в точке пересечения наклонной фермы опорной башни со стойкой, то для башен простой треугольной конфигурации величина этого угла может быть с достаточной степенью точности принята равной углу между горизонталью и наклонной фермой.

Входящая в эти уравнения величина является переменной, зависящей не только от первоначального натяжения рабочих тросов, но и от положения и веса груза в пролете.

Из уравнения (45а) можно установить, что при перемещении тележки в направлении от некачающейся башни к качающейся величина Alx сначала постепенно увеличивается, достигая максимума при положении груза примерно около середины пролета, затем постепенно падает и при приближении тележки к качающейся башне становится отрицательной (башня наклоняется в сторону от пролета), достигая максимума при положении тележки у головки башни (х=1). Малые величины последних двух членов уравнения (45а) определяют при этом соответственно малую величину отрицательного значения Мх, которую практически можно не учитывать, принимая, что качание башни происходит внутрь пролета, т. е. в одну сторону от вертикали, принятой за ее исходное положение. Это условие отображено в упрощенных уравнениях (456) и (45в), согласно которым величина Д4 изменяется от нуля (при тележке, расположенной у некачающейся башни) до максимума (при тележке, установленной точно в середине пролета) и снова до нуля (при подходе тележки к качающейся башне).

Следует, однако, заметить, что при этом, по мере наклонения качающейся башни внутрь пролета, возникает все большее одностороннее давление на подкрановые пути. Поэтому на практике за исходное (монтажное) положение башни обычно принимают такое, при котором задняя стойка ее наклонена и головка находится вне пролета вследствие некоторого увеличения длины каната. Пересчет натяжения каната при этом, как правило, не производится, хотя оно несколько изменяется вследствие изменения плеч всех приложенных к башне сил.

Ход расчета несущего каната кабельного крана с качающейся башней сводится к следующему.

Случай 3 — оба конца каната закреплены.

В этом случае несущему канату при монтаже придают первоначальное натяжение, которое затем регулируется по мере необходимости с помощью винтового натяжного устройства или полиспаста. При таком закреплении каната натяжение его меняется в больших пределах в зависимости от соотношения веса тележки с грузом и веса канатов, положения тележки в пролете и температурных колебаний. Наибольшее натяжение каната возникает при положении груженой тележки по середине пролета и при наиболее низкой окружающей температуре. По мере перемещения груженой тележки от середины пролета к опорам натяжение каната может падать на 30—40%, а изменение нагрузки на канат (например, при разгрузке тележки) так же, как и изменение температурных условий (по отношению к монтажным), могут снизить натяжение несущего каната более чем вдвое.

Как указывалось ранее, нагрузка несущего каната составляется из равномерно распределенной нагрузки (от его собственного веса и веса поддержек с опирающимися на них рабочими канатами) и из сосредоточенной нагрузки (от веса грузовой тележки с грузом или без груза).

Нагрузка передается не только на несущий канат, но и на пучок рабочих канатов, соединенных с несущим канатом поддержками. Распределение нагрузки должно происходить пропорционально натяжениям несущего каната и пучка рабочих канатов и пропорционально модулям упругости этих канатов.

Натяжения канатов, в свою очередь, пропорциональны их погонным весам и обратно пропорциональны принятым запасам прочности на разрыв.

Таким образом, пучок рабочих канатов принимает на себя от 2,5 до 6% нагрузки. Такое незначительное участие пучка рабочих канатов в восприня-тии поперечной нагрузки позволяет пренебречь им и считать, что вся нагрузка воспринимается несущим канатом.

Для определения натяжения несущего каната рассмотрим два состояния:
1) когда грузовая тележка с максимальным грузом общим весом Qm находится на середине пролета, загруженного равномерно распределенной нагрузкой gm (рис. 49, а), а температура каната равна t°m (в этом случае несущий канат длиной sm имеет максимальное расчетное натяжение Тт);
2) когда грузовая тележка с произвольным грузом общим весом Qx находится на расстоянии х от башни; равномерно распределенная нагрузка на канат составляет gx (рис. 49, б), а

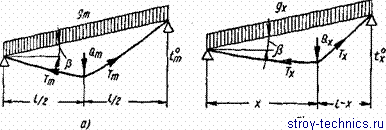
Рис. 49. Схема нагружения Несущего каната с двумя закрепленными концами.

В случаях, когда концы несущих канатов закреплены вне башен или на мачтах с гибкими оттяжками, расчет также можно вести по уравнениям (48) и (48а) (при обычном расположении оттяжек под углами около 35—45° к горизонту ошибка не превышает 5%). Однако в случаях, когда несущий канат закрепляется вне опорных башен на большом расстоянии от них, влиянием участков его за пределами рабочего пролета пренебрегать не следует. В этих случаях расчет может производиться по той же методике, как и для рассмотренного ранее случая расчета каната с обоими концами, закрепленными неподвижно на башнях, т. е. с использованием уравнений (47а) и (476), но с учетом длины каната при определении величин sm и s как суммы участков в пролете и за башнями.

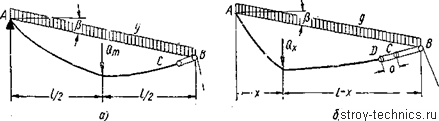
Рис. 50. Схемы нагружения несущего каната, спускаемого с помощью полиспаста.

Таким образом, для рассматриваемого случая также могут быть использованы зависимости, выведенные в предыдущей главе.